I remember that when the STL came out, vectors were quite a surprising new way to approach dynamic arrays. In this post we'll look at some of the implications of applying the vector 'paradigm' to a more involved data structure, the dynamic mesh.

We do a load of mesh processing at PathEngine, both during content-processing and at SDK run-time.

Sometimes this involves modifying the mesh, and we need dynamic mesh data structures to support this.

We started out using a traditional pointer-based, 'list-like' mesh data structure, but switched to a 'vector-like' approach, based on contiguous buffers, and from iterators to direct indexing..

Related posts

This post is part of a series of posts about vectors and vector based containers, and also a series of posts about how we use meshes in PathEngine.

We'll be using the idea of 'vector hosted lists' and the cVectorWithDeadEntries class introduced in this previous post.

Background

So we have a lot of mesh related code.

Some of this needs to modify the mesh (to build ground meshes at content processing time, for example), but a lot of it just needs to operate on the mesh, without any changes to the mesh structure (to generate some run-time query result, for example).

Static and dynamic meshes

When modifying the mesh we're going to need some kind of dynamic mesh data representation.

The traditional approach is to use something like a 'winged-edge' or 'half-edge' pointer-based data structure.

The interfaces to these data structures is usually presented through a set of iterators, which wrap internal pointers to things like faces, edges and vertices. Without additional index creation it's generally not possible to access these internal elements in a random-access or indexed fashion.

If we don't need to modify a mesh, a much more concise and efficient representation is possible. (Let's call this a static mesh.)

For example the data members for a static tri-mesh (without any contained data) might be defined, in c++, as follows:

#include <vector>
#include <cstdint>

class cTriMesh
{
  // {twin edge, edge vert} * 3 * number of tris
    std::vector<int32_t> _edgeInfo;
  // the first edge around each vertex
    std::vector<int32_t> _vertFirstEdge;

//... rest of class implementation
};

(This represents the connectivity between a set of faces, edges and vertices, for the specific case where all faces have exactly 3 edges, with edges stored in face order and the mapping between edges and faces then implicit in this ordering.)

With this kind of static mesh setup, we can usually choose how we access the mesh, in particular with it now possible to use direct element indexing, as well as iterator based access.

Common requirements, need for shared interface

When modifying the mesh we have to use a dynamic mesh, but at run-time we need best performance and minimal memory footprint, and that means a static mesh.

So modifying and non-modifying mesh code will naturally operate on different concrete data structures.

But it turns out there's a lot of commonality between these two sets of code.

There are a bunch of basic mesh operations required in both cases.

One example is mesh traversal (as discussed here), but there's also a bunch of other, lower level stuff that is nice to factor out.

And there are also some high level operations that we would like to apply in different contexts, and to both dynamic and static meshes. (For example, some retriangulation and partitioning operations.)

We don't want to write and maintain multiple versions of all this shared code, so we need to choose some common interface that abstracts away from the actual concrete data structure being used.

Advantages of indexing

Iterator based interfaces are pretty cool if you have to use pointer based data structures.

If you're writing code that might be applied to either std::list or std::vector, for example, it's great to be abstract away the differences between these representations.

But, if you know you're only ever going to use vectors (or other indexable data structures), there can be some significant advantages to dropping this level of abstraction, and just using indexes directly:

• Indexes can be written and read directly to and from persistence.
• Random access through direct indexing can open up additional algorithmic possibilities.
• Indexes can be used as element references across multiple parallel data structures.
• Indexes can be more space efficient, and help reduce code dependencies.
• Unlike pointers or pointer-based iterators, indexes remain valid across buffer reallocation.

There can be other factors to take into account, and there are also reasons why an iterator based interface might still be a better choice, depending on the situation, but for PathEngine a common mesh interface based on direct indexing is preferable, if this is possible.

Performance

Because of the way modern CPUs work data structures based on contiguous buffers (such as std::vector) tend to outperform data structures with per-element allocations (such as std::list).

I talked about this in more detail in this previous blog post, so please refer to that post (and the linked articles) for more detailed discussion, but the key points are really just that contiguous data is more cache friendly and that a smaller number of (contiguous) buffers will tend to incur less memory overhead and fragmentation.

If you look back at our cTriMesh class you'll note that we actually get by with just two allocated memory buffers, in this specific case. That's going to be a whole lot more efficient than per element allocations.

Lets see if we can generalise the approach taken for cTriMesh, and come up with some alternative dynamic mesh representations with a bit of that 'vector sauce'!

Vector meshes 1.0

A key idea of std::vector is to focus on the specific case of adding elements at the end (with push_back()), and to optimise for this at the expense of more general modification.

The data buffers for cTriMesh are already implemented with vectors, internally, and we can leverage these internal vectors for some 'push_back()' style functionality.

For simplicity we'll ignore some integer type and range details, and just use a single integer type, (int32_t), for everything (we'll come back to this point later on):

#include <cassert>
#include <vector>
#include <cstdint>

class cTriMesh
{
  // {twin edge, edge vert} * 3 * number of tris
    std::vector<int32_t> _edgeInfo;
  // the first edge around each vertex
    std::vector<int32_t> _vertFirstEdge;
public:

    int32_t
    twin(int32_t edge) const
    {
        return _edgeInfo[edge * 2];
    }
    int32_t
    vert(int32_t edge) const
    {
        return _edgeInfo[edge * 2 + 1];
    }

    int32_t
    edges() const
    {
        return _edgeInfo.size() / 2;
    }

    int32_t
    addTri(int32_t v1, int32_t v2, int32_t v3)
    {
        // cannot be called after verts initialised
        assert(_vertFirstEdge.empty());
        int32_t newFaceIndex = _edgeInfo.size();
        // no twins, initially
        _edgeInfo.push_back(-1);
        _edgeInfo.push_back(v1);
        _edgeInfo.push_back(-1);
        _edgeInfo.push_back(v2);
        _edgeInfo.push_back(-1);
        _edgeInfo.push_back(v3);
        return newFaceIndex;
    }

    void
    connectEdges(int32_t edge1, int32_t edge2)
    {
        // cannot be called after verts initialised
        assert(_vertFirstEdge.empty());
        // the edges should be unconnected, initially
        assert(twin(edge1) == -1);
        assert(twin(edge2) == -1);
        // can't connect an edge to itself
        assert(edge1 != edge2);
        _edgeInfo[edge1 * 2] = edge2;
        _edgeInfo[edge2 * 2] = edge1;
    }

    void
    initVerts()
    {
        assert(_vertFirstEdge.empty());
        int32_t verts = 0;
        for(int32_t e = 0; e != edges(); ++e)
        {
            if(vert(e) >= verts)
            {
                verts = vert(e) + 1;
            }
        }
        // first pass assigns any external edges as first edge
        _vertFirstEdge.resize(verts, -1);
        for(int32_t e = 0; e != edges(); ++e)
        {
            if(twin(e) == -1)
            {
                assert(_vertFirstEdge[vert(e)] == -1);
                _vertFirstEdge[vert(e)] = e;
            }
        }
        // second pass needed if there are any internal vertices
        for(int32_t e = 0; e != edges(); ++e)
        {
            if(_vertFirstEdge[vert(e)] == -1)
            {
                _vertFirstEdge[vert(e)] = e;
            }
        }
    }

    int32_t
    vertFirstEdge(int32_t edge) const
    {
        // cannot be called before verts initialised
        assert(!_vertFirstEdge.empty());
        return _vertFirstEdge[edge];
    }
};

This gives us a kind of 'builder' interface for triangle mesh construction, for situations where we already have an enumerated set of vertices to build around (which turns out to be quite a common case, in PathEngine).

Mesh construction

It's a pretty minimal class definition, and other accessors and helpers would certainly be useful, but it's enough to support some simple mesh construction code. For example, we can build a simple square mesh, composed of two triangles, as follows:

int
main(int argc, char* argv[])
{
    cTriMesh square;
    square.addTri(0, 1, 2);
    square.addTri(3, 0, 2);
    square.connectEdges(2, 4);
    square.initVerts();
    // vert connectivity available from here
    assert(square.vertFirstEdge(2) == 5);
    return 0;
}

Variations

With a bit of work, this approach can be extended to polygonal meshes (i.e. with arbitrary edges per face), and we can also take different approaches to the way vertex connectivity is handled (e.g. verts enumerated automatically based on edge connectivity), but the key idea is just that we stick with 'adding stuff on the end', and we're essentially then stuck with some kind of separate initVerts() step, if vertex connectivity is required.

Application

So this is a pretty simple idea, but simple is good. And it's definitely a good idea to consider this kind of simple 'add it on the end' vector mesh implementation before reaching out for more general dynamic mesh capabilities.

In PathEngine, we use this kind of interface for building mesh triangulations, for example, and for mesh construction from persistence. (It's pretty efficient, especially if you add a reserve() call, and more flexible than low level binary persistence with regards to compatibility across format changes.)

A big advantage is also the fact that you just need to shrink to fit, and you can go straight on and use the constructed mesh as a run-time mesh with essentially no overhead for the incremental construction.

Sometimes you want to do more than just construct meshes, however.

In some cases it's possible to reformulate mesh modifying algorithms in terms of copying off part of a mesh, or otherwise constructing a new mesh for some modified mesh result (sometimes this can even be a big win, immutable data and functional programming for the world!).

But in other situations this may not be feasible (or efficient), and sometimes you just need to make arbitrary mesh modifications that don't fit in with this kind of construction interface.

Let look at how we can take things a bit further, while still working with vector buffers, to tackle some 'real' dynamic mesh modification!

Vector meshes 2.0

The solution will build directly on the idea of 'vector hosted lists' and the cVectorWithDeadEntries container class described here.

cVectorWithDeadEntries is essentially a buffer of integer type elements, that supports marking individual elements as 'dead', and maintains a free list of dead elements so that dead elements can be trivially found and reused.

Three vector hosted lists

We'll need three cVectorWithDeadEntries instances, one for each of the three index types (face, edge and vertex).

class cDynamicMesh
{
    cVectorWithDeadEntries _faceFirstEdge;
    cVectorWithDeadEntries _nextEdge;
    cVectorWithDeadEntries _vertFirstEdge;

  // other edge data components
  // {twin, face, vert, prev} * number of edges
    cVector<int32_t> _edgeData;

//... rest of class implementation
};

This gives us a way to keep track of each of: dead edges, dead faces and dead verts. Elements of each type can be marked as dead when no longer needed, and we can also use the relevant cVectorWithDeadEntries instance to quickly obtain new elements of each type when required.

Converting pointer-based dynamic mesh code to cDynamicMesh

We end up with something similar to the pointer-based half-edge data structure I referenced at the top of the post, but with free-lists in cVectorWithDeadEntries replacing more general element memory allocation.

You can think of this as a 'vector hosted half-edge representation', if you like.

And then, if you have some code for manipulating a (pointer-based) half edge data structure, it's now pretty straightforward to port this to cDynamicMesh.

Specifically, each time we would normally allocate an element, we now make a call into cVectorWithDeadEntries::addEntry(), and each time we would normally delete an element, we now make a call into cVectorWithDeadEntries::markAsDead().

There's some extra edge related data to take care of, in _edgeData, and we'll need to take some extra steps just to ensure that the size of this vector always corresponds to _nextEdge.size() * 4.

Example code

Let's see this in practice!

We'll set up some mesh construction methods for cDynamicMesh.

This time, vertices will get updated and stay valid as triangles are added. And we'll also add in some method calls for disconnecting and deleting faces:

class cDynamicMesh
{
    cVectorWithDeadEntries _faceFirstEdge;
    cVectorWithDeadEntries _nextEdge;
    cVectorWithDeadEntries _vertFirstEdge;

  // other edge data components
  // twin, face, vert, prev
    std::vector<int32_t> _edgeData;

    int32_t&
    edgeTwin(int32_t e)
    {
        return _edgeData[e * edgeDataItems()];
    }
    int32_t&
    edgeFace(int32_t e)
    {
        return _edgeData[e * edgeDataItems() + 1];
    }
    int32_t&
    edgeVert(int32_t e)
    {
        return _edgeData[e * edgeDataItems() + 2];
    }
    int32_t&
    edgePrev(int32_t e)
    {
        return _edgeData[e * edgeDataItems() + 3];
    }

    static int32_t edgeDataItems() {return 4;}

    int32_t
    newEdgeAndVert(int32_t face)
    {
        int32_t sizeBefore = _nextEdge.size();
        int32_t e = _nextEdge.addEntry();
        int32_t sizeAfter = _nextEdge.size();
        if(sizeAfter != sizeBefore)
        {
            _edgeData.resize(sizeAfter * edgeDataItems());
        }
        edgeTwin(e) = -1;
        edgeFace(e) = face;
        int32_t v = _vertFirstEdge.addEntry();
        _vertFirstEdge.setValue(v, e);
        edgeVert(e) = e;
        return e;
    }

    void
    chainEdges(int32_t edgeBefore, int32_t edgeAfter)
    {
        _nextEdge.setValue(edgeBefore, edgeAfter);
        edgePrev(edgeAfter) = edgeBefore;
    }

    void
    updateVertBeforeBreakEdge(int32_t e1)
    {
        int32_t v1 = vert(e1);
        if(twin(_vertFirstEdge[v1]) != -1)
        {
        // v1 was internal, no vertex break required
            _vertFirstEdge.setValue(v1, e1);
            return;
        }
        // v1 was external
        // so it is now broken into two vertices
        int32_t newVert = _vertFirstEdge.addEntry();
        _vertFirstEdge.setValue(newVert, e1);
        // tell edges now assigned to newVert about the change
        int32_t e = e1;
        do
        {
            edgeVert(e) = newVert;
            e = twin(prev(e));
        }
        while(e != -1 && e != e1);
    }

public:

    int32_t
    twin(int32_t e) const
    {
        return _edgeData[e * edgeDataItems()];
    }
    int32_t
    face(int32_t e) const
    {
        return _edgeData[e * edgeDataItems() + 1];
    }
    int32_t
    vert(int32_t e) const
    {
        return _edgeData[e * edgeDataItems() + 2];
    }
    int32_t
    prev(int32_t e) const
    {
        return _edgeData[e * edgeDataItems() + 3];
    }

    int32_t
    next(int32_t edge) const
    {
        return _nextEdge[edge];
    }

    int32_t
    faceFirstEdge(int32_t f) const
    {
        return _faceFirstEdge[f];
    }
    int32_t
    vertFirstEdge(int32_t v) const
    {
        return _vertFirstEdge[v];
    }

    int32_t
    addTri()
    {
        int32_t newF = _faceFirstEdge.addEntry();
        int32_t e1 = newEdgeAndVert(newF);
        int32_t e2 = newEdgeAndVert(newF);
        int32_t e3 = newEdgeAndVert(newF);
        chainEdges(e1, e2);
        chainEdges(e2, e3);
        chainEdges(e3, e1);
        _faceFirstEdge.setValue(newF, e1);
        return newF;
    }

    void
    connectEdges(int32_t e1, int32_t e2)
    {
        edgeTwin(e1) = e2;
        edgeTwin(e2) = e1;
        int32_t v = vert(e1);
        if(v != vert(next(e2)))
        {
          // keep the vert at start of e1,
          // reassign the edges around from next(e2)
          // to this vert
            int32_t v_ToDelete = vert(next(e2));
            _vertFirstEdge.setValue(v, _vertFirstEdge[v_ToDelete]);
            int32_t e = next(e2);
            while(1)
            {
                edgeVert(e) = v;
                e = twin(e);
                if(e == -1)
                {
                    break;
                }
                e = next(e);
            }
            _vertFirstEdge.markAsDead(v_ToDelete);
        }
        v = vert(e2);
        if(v != vert(next(e1)))
        {
          // keep the vert at end of e1,
          // reassign the edges around from e2
          // to this vert
            int32_t v_ToDelete = v;
            v = vert(next(e1));
            int32_t e = e2;
            while(1)
            {
                assert(vert(e) == v_ToDelete);
                edgeVert(e) = v;
                e = twin(prev(e));
                if(e == -1)
                {
                    break;
                }
            }
            _vertFirstEdge.markAsDead(v_ToDelete);
        }
    }

    void
    disconnectEdges(int32_t e)
    {
        int32_t twinE = twin(e);
        assert(twinE != -1);
        updateVertBeforeBreakEdge(e);
        updateVertBeforeBreakEdge(twinE);
        edgeTwin(e) = -1;
        edgeTwin(twinE) = -1;
    }

    void
    deleteFace(int32_t faceToDelete)
    {
        int32_t firstE = _faceFirstEdge[faceToDelete];
    // disconnect any connected edges
        int32_t e = firstE;
        do
        {
            if(twin(e) != -1)
            {
                disconnectEdges(e);
            }
            e = next(e);
        }
        while(e != firstE);
    // delete verts
        e = firstE;
        do
        {
            _vertFirstEdge.markAsDead(vert(e));
            e = next(e);
        }
        while(e != firstE);
    // delete edges
        e = firstE;
        do
        {
            int32_t toDelete = e;
            e = next(e);
            _nextEdge.markAsDead(toDelete);
        }
        while(e != firstE);
    // delete face
        _faceFirstEdge.markAsDead(faceToDelete);
    }
};

Again, it's quite a minimal class definition, for conciseness. I've left out a bunch of assertions (that could help guard against invalid calls), and other accessors and helpers would be useful. But this nevertheless shows some real dynamic mesh operations in action.

Constructing a cDynamicMesh

Here's updated code for building that simple square mesh:

int
main(int argc, char* argv[])
{
    cDynamicMesh mesh;
    int32_t f1 = mesh.addTri();
    int32_t f2 = mesh.addTri();
    int32_t e1 = mesh.prev(mesh.faceFirstEdge(f1));
    int32_t e2 = mesh.next(mesh.faceFirstEdge(f2));
    mesh.connectEdges(e1, e2);
    // vert connectivity always available
    // (no initVerts call required)
    assert(mesh.vertFirstEdge(2) == 5);
    return 0;
}

This has changed a bit. We're no longer making assumptions about what indexes get assigned to elements, for one thing. This is more in the spirit of dynamic mesh modifying code, where we wouldn't be able to predict these indexes, and avoids assumptions about the exact internal behaviour of cDynamicMesh::addTri().

And construction no longer assumes a pre-existing framework for vertices. Instead, vertices get added and deleted as necessary to maintain vertex to edge connectivity as the mesh is modified.

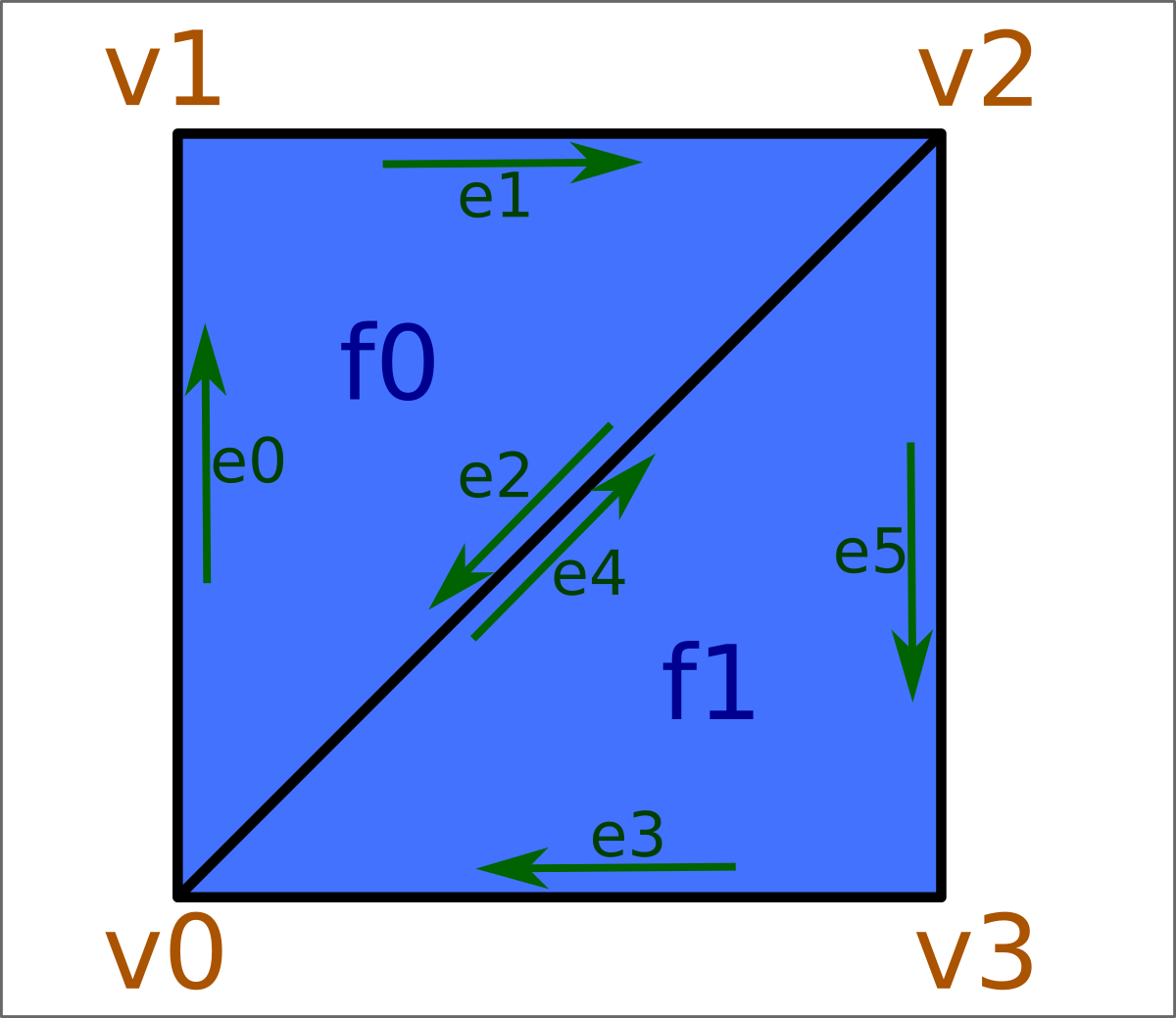
Six vertices actually then get created, initially, by the two calls to cDynamicMesh::addTri():

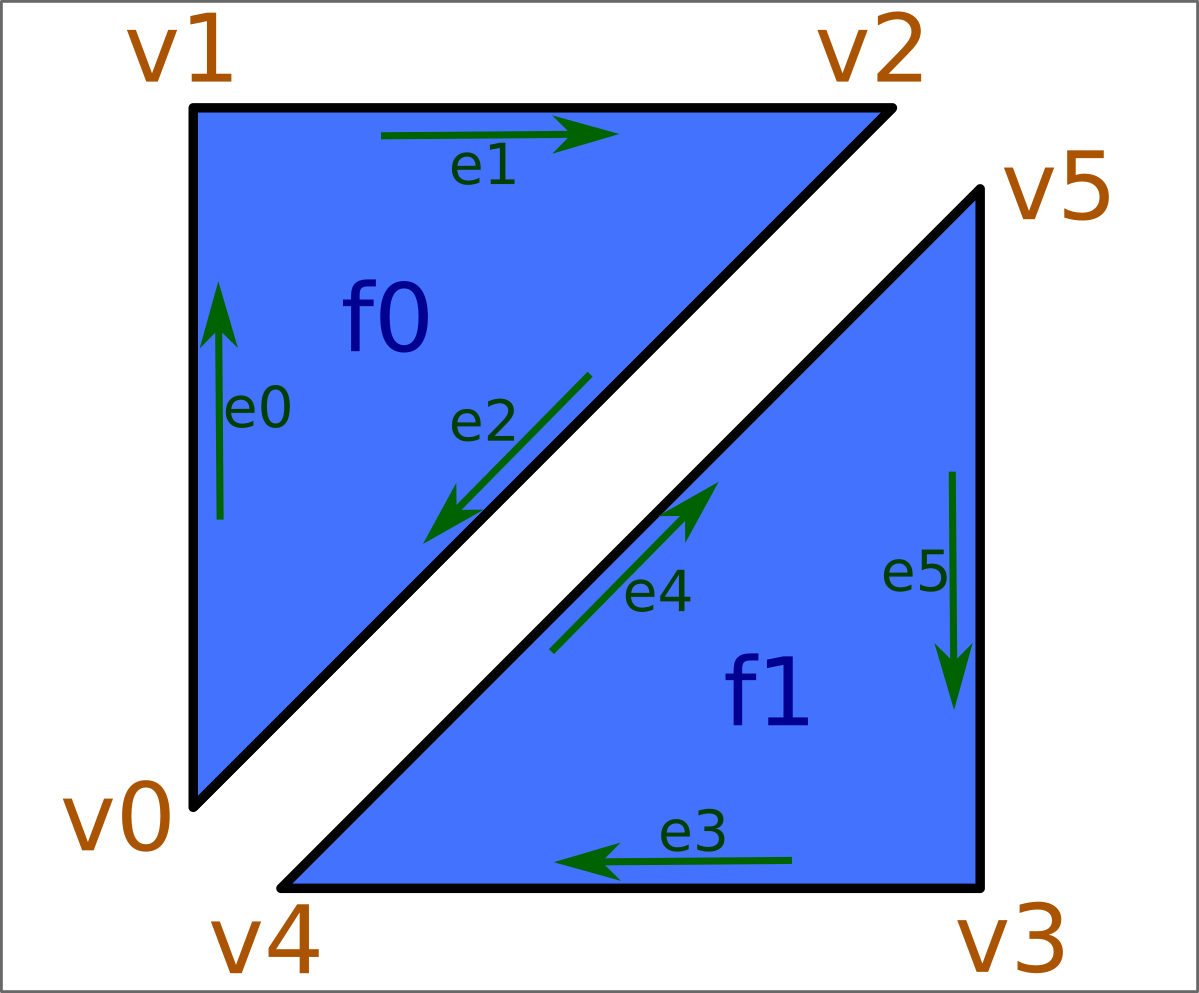
And then two of these vertices are deleted (marked as dead) in the call to cDynamicMesh::connectEdges():

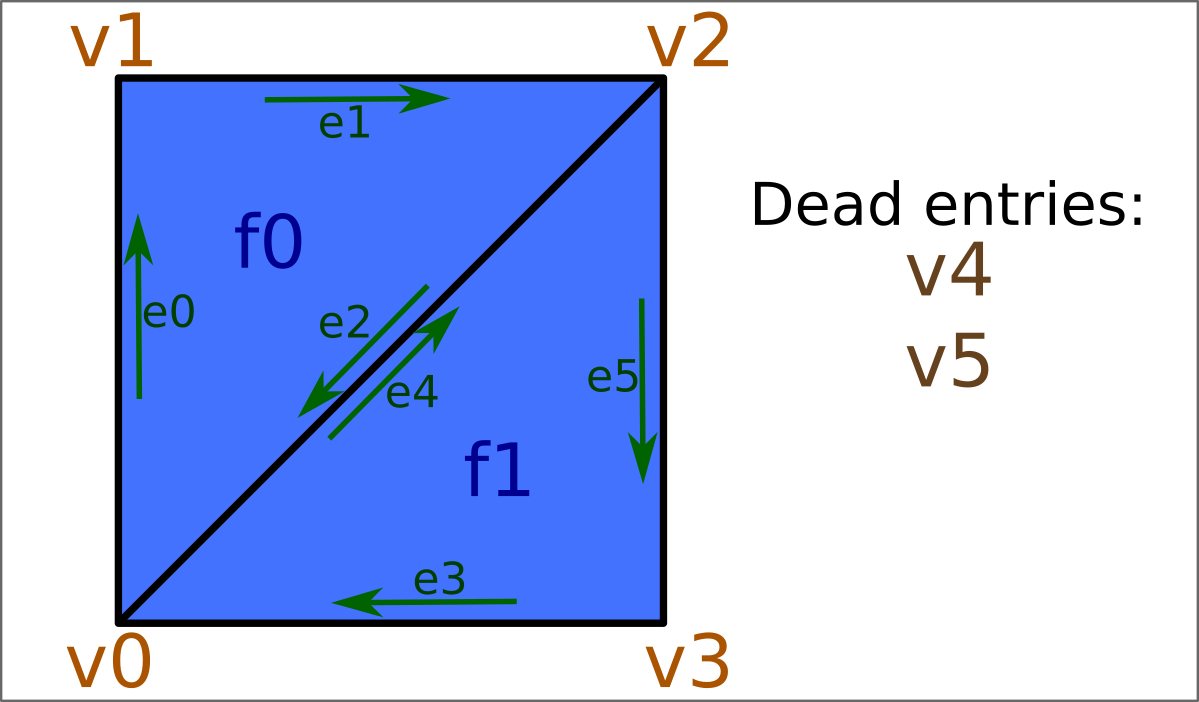
This is less efficient, of course, if you are actually just adding faces in order for mesh construction, but this is now 'real' dynamic mesh code. Faces can be added more dynamically, with other arbitrary mesh based code mixed in around addTri calls, and vertex connectivity maintained correct through.

Consolidate

As with the underlying cVectorWithDeadEntries class, it can be a good idea to periodically collapse the mesh down to remove any dead entries. At PathEngine we actually do this by calling consolidate on the underlying face and vertex cVectorWithDeadEntries, and remapping edges to run in face order.

Indexing

The classes I've posted use an interface based on directly specifying mesh elements by index value, and this is also essentially what we do at PathEngine.

To some extent the iterators/indexes choice is independent of the vector/list like mesh choice, and I think it makes sense to use these kind of vector mesh data structures in most cases even if you decide to stick with iterators. (It's certainly possible to provide an iterator-based interface to these classes.)

But the possibility to use direct indexing is pretty key to the way we use meshes at PathEngine. (We'll see a bit more about why in a future post!)

A raw integer is perhaps not the best choice for our index types, however, so let's see if we can improve on that. We'll also go on to look at some of the implications of an index-based interface in general.

Safer index types

One problem with cTriMesh and cDynamicMesh, as currently written, is that there's nothing to stop us passing an index to one element (say a face) into an interface method expecting an index to a different kind of element.

int
main(int argc, char* argv[])
{
    cDynamicMesh mesh;
    int32_t f1 = mesh.addTri();
    int32_t f2 = mesh.addTri();
    // ** bad things happen here!
    mesh.connectEdges(f1, f2);
    return 0;
}

Adding assertions in connectEdges() to check that the index values are in range and that the corresponding edges are not already connected will help, but it's even better if we can get the compiler to differentiate between indexes to different element types, and tell us if we try to pass the wrong type.

And note that valid element indexes are always positive, with -1 reserved as an invalid element index value (returned, for example, if you call twin() on a disconnected edge).

We'll use the following template class to wrap this up, and generally define the set of supported operations on mesh index values:

template <class tTag>
class cMeshIndex
{
    int32_t _value;
    typedef cMeshIndex<tTag> tThis;
public:

    cMeshIndex() {}
    explicit cMeshIndex(int32_t value) :
     _value(value)
    {
        assert(value >= -1);
    }

    int32_t
    extractInt() const
    {
        assert(isValid());
        return _value;
    }

    bool
    isValid() const
    {
        return _value >= 0;
    }
    static tThis
    constructInvalid()
    {
        tThis result;
        result._value = -1;
        return result;
    }

    tThis& operator++()
    {
        ++_value;
        return *this;
    }
    tThis operator++(int)
    {
        tThis temporary = *this;
        ++*this;
        return temporary;
    }
    tThis& operator--()
    {
        --_value;
        return *this;
    }
    tThis operator--(int)
    {
        tThis temporary = *this;
        --*this;
        return temporary;
    }
    tThis operator+(tThis rhs) const
    {
        return tThis(_value + rhs._value);
    }
    tThis operator-(tThis rhs) const
    {
        assertD(_value >= rhs._value);
        return tThis(_value - rhs._value);
    }
    bool
    operator==(tThis rhs) const
    {
        return _value == rhs._value;
    }
    bool
    operator!=(tThis rhs) const
    {
        return _value != rhs._value;
    }
    bool
    operator<(tThis rhs) const
    {
        return _value < rhs._value;
    }
    bool
    operator<=(tThis rhs) const
    {
        return _value <= rhs._value;
    }
    bool
    operator>(tThis rhs) const
    {
        return _value > rhs._value;
    }
    bool
    operator>=(tThis rhs) const
    {
        return _value >= rhs._value;
    }
};

Note that operations such as multiply and divide are not supported, as we usually won't want to do these things with our mesh index values.

cMeshIndex is templated by some other 'tag' class, cTag, but we don't refer to cTag in the implementation. The sole purpose of this tag class is to provide a way to set up different versions of cMeshIndex for each of our mesh element types:

class cMeshIndex_Face_Tag {};
class cMeshIndex_Edge_Tag {};
class cMeshIndex_Vert_Tag {};
typedef cMeshIndex<cMeshIndex_Face_Tag> tFace;
typedef cMeshIndex<cMeshIndex_Edge_Tag> tEdge;
typedef cMeshIndex<cMeshIndex_Vert_Tag> tVert;

It's pretty straightforward to then rewrite our mesh classes to accept and return the correct index types, for example:

    tEdge
    twin(tEdge e) const
    {
        return tEdge(_edgeData[e.extractInt() * edgeDataItems()]);
    }
    tFace
    face(tEdge e) const
    {
        return tFace(_edgeData[e.extractInt() * edgeDataItems() + 1]);
    }
    tVert
    vert(tEdge e) const
    {
        return tVert(_edgeData[e.extractInt() * edgeDataItems() + 2]);
    }
    tEdge
    prev(tEdge e) const
    {
        return tEdge(_edgeData[e.extractInt() * edgeDataItems() + 3]);
    }

    tEdge
    next(tEdge edge) const
    {
        return tEdge(_nextEdge[edge.extractInt()]);
    }

With overloading, we can even leverage these types to simplify our interface a bit:

    //int32_t
    //faceFirstEdge(int32_t f) const
    //{
    //    return _faceFirstEdge[f];
    //}
    //int32_t
    //vertFirstEdge(int32_t f) const
    //{
    //    return _vertFirstEdge[f];
    //}
    tEdge
    firstEdge(tFace f) const
    {
        return tEdge(_faceFirstEdge[f.extractInt()]);
    }
    tEdge
    firstEdge(tVert v) const
    {
        return tEdge(_vertFirstEdge[v.extractInt()]);
    }

If we update the signatures for addTri() and connectEdge(), also, we should now get a compiler error in that buggy code:

int
main(int argc, char* argv[])
{
    cDynamicMesh mesh;
    auto f1 = mesh.addTri();
    auto f2 = mesh.addTri();
    // ** compiler says no!
    // ** (types don't match)
    mesh.connectEdges(f1, f2);
    return 0;
}

This is simple, and works pretty well for keeping things sane in a lot of mesh based code.

Note that this doesn't stop us using index values from one mesh in calls to another, however. You have to be quite careful, in particular, if you're writing code that operates on more than one mesh at the same time (for mesh comparison, for example), But the fact that the index types are independent of any specific mesh container can also be a big advantage, in some other situations.

Dependencies

The fact that we can define index types completely independently of the container indexed container (even with cMeshIndex) is also a big advantage. Compared to an iterator based interface, we've found that indexing is something that enables us to hugely reduce code dependencies.

Conciseness

With an index based interface many calls end up requiring the container plus an index, in situations where iterators would otherwise often be able to handle the call all by themselves, and this is something that can affect useability.

For example, in situations where we would previously call something like edgeIt.next().twin() we now need to use the (clumsier) form mesh.twin(mesh.next(edge)).

You could use iterators and indexes to try to get the best of both worlds, but that adds other complications (e.g. do we pass iterators or indexes?) but we found that just using indexes pretty much everywhere seems to work out cleaner overall.

Wrapping up common sequences of accessors can then help with this issue, to some extent, e.g.:

template <class tMesh> tEdge
TwinNext(const tMesh& mesh, tEdge e)
{
    return mesh.next(mesh.twin(e));
}
template <class tMesh> tEdge
TwinPrev(const tMesh& mesh, tEdge e)
{
    return mesh.prev(mesh.twin(e));
}
template <class tMesh> tEdge
PrevTwin(const tMesh& mesh, tEdge e)
{
    return mesh.twin(mesh.prev(e));
}
template <class tMesh> tEdge
NextTwin(const tMesh& mesh, tEdge e)
{
    return mesh.twin(mesh.next(e));
}
template <class tMesh> tEdge
NextTwin(const tMesh* mesh, tEdge e)
{
    return NextTwin(*mesh, e);
}
template <class tMesh> tEdge
NextNext(const tMesh& mesh, tEdge e)
{
    return mesh.next(mesh.next(e));
}

Loops

Looping through elements is a bit clunkier now, and we basically have to do something like the following:

template <class tMesh> void
LoopThroughFaces_Indexes(tMesh& m)
{
    for(tFace f(0); f != m.faceSize(); ++f)
    {
        if(m.entryIsDead(f)
        {
            continue;
        }
        //.. do stuff
    }
}

instead of something like (with iterators):

template <class tMesh> void
LoopThroughFaces_Iterators(tMesh& m)
{
    for(auto i = m.beginFace();  i != m.endFace(); ++i)
    {
        //.. do stuff
    }
}

(Note that this depends on some additional interface methods, faceSize() and entryIsDead(), not shown above but straightforward to add.)

Mesh contents

You probably noticed by now that neither of the mesh classes in this post actually contain any data.

A vector is templated by the type of its contents, and these contents can then be accessed either directly, or through iterator dereferencing.

To be really 'vector-like' you'd expect a vector mesh to do something similar, but with three template content type parameters, and three different sets of data (so that you can store data per-face, per-edge, and per-vertex).

This is what we did previously, in fact. but I think there's a better way to set this up, so I'm not going to go into this issue in more detail in this post.

I'll talk a bit more about what we actually do now to organise per-element mesh data, in a future post!

Conclusion

As well as being list-like, mesh data structures can also be vector-like, even if you need full support for dynamic modification.

Being vector-like has advantages for performance, and also in terms of memory allocation overhead and fragmentation, and vector-like data structures give you the option to use direct indexing as well as (or instead of) iterators.

This is not just applicable to meshes. The same approach can be used to convert other pointer-based data structures. In general, if you think you have to use pointer links, think again.

Try to keep a bottle of that lovely vector sauce somewhere close to hand. Maybe you can 'just add stuff at the end', or maybe there's room for creative application of some vector hosted lists..